Задание к ТР   по линейной алгебре

 

Часть 1.

Придумать невырожденную матрицу А третьего порядка. Решить для неё следующие задачи.

 

 

1.Разложить матрицу А на произведение элементарных матриц.

2.Вычислить  det A, используя определение функции det.

3.Вычислить  det A, приведя А к треугольной матрице.

4.Вычислить   det A с помощью разложения по какой-то строке.

5.Вычислить  det A c  помощью разложения по какому-то столбцу.

6.Найти обратную матрицу, исходя из её разложения на произведение  элементарных матриц.

7.Найти обратную матрицу по расширенной матрице (А|E).

8.Найти обратную матрицу с помощью адъюнктов.

9.Решить  систему уравнений   Ах=b методом обратной  матрицы  (b=d₉   из части второй ТР )

10.Решить  систему уравнений Ax=b методом Гаусса.

11.Решить  систему уравнений Аx=b методом Крамера.

 

Часть 2.

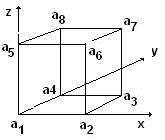
Пусть Е=[0,1]³  -   единичный куб, вершины  a_i  которого обозначены так. как показано на рисунке:

 

 

Пусть:

 l₁=a₁a₂, l₂=a₂a₃, l₃=a₃a₄, l₄=a₄a₁, l₅=a₅a₆,l₆=a₆a₇,l₇=a₇a₈, l₈=a₈a₅, l₉=a₁a₅, l₁₀=a₂a₆, l₁₁=a₃a₇, l₁₂=a₄a₈ –

рёбра куба Е,

l₁₃=a₁a₇, l₁₄=a₂a₈, l₁₅=a₃a₅, l₁₆=a₄a₈ – диагонали куба Е,  a₉ – пересечение диагоналей.

Рассмотрим множества D=A(E), d_i=A(a_i), L_i=A(l_i), X=A^-1(E). (Здесь А – линейная функция с матрицей А.)

Будем считать, что D – жёсткое тело, невесомое во всех своих частях за исключением точек d_i, i=1,…,9,

в которых сосредоточены массы m_i (задать  m_i  самостоятельно).  Найти:

1. Уравнения прямых, на которых лежат рёбра и диагонали.

2. Уравнения плоскостей, на которых лежат грани (в трёх основных формах).

3. Длины рёбер и диагоналей.

4. Площади граней (используя векторное произведение и определитель Грама).

5. Объём V_D  (используя смешанное произведение и определитель Грама).

6. Центр тяжести Ц=(x*, y*, z*) по формулам:

 

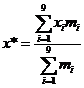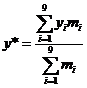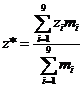      ,      ,      .  Здесь d_i = (x_i, y_i, z_i ).

7. Объём V_X.  Убедиться, что    .

8, Момент силы тяжести относительно начала координат.

 

Часть 3.

 

Числа s_{ij ,}  вычисляемые по формулам:

 

,  , ,

 

, , 

 

называются моментами инерции тела D.   Они составляют симметрическую матрицу S,   которая называется тензором инерции тела  D:

 

.

 

 

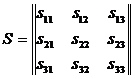Множество Э={(x,y,z)| s₁₁x² + s₂₂y² + s₃₃z² + 2 s₁₂xy + 2s₁₃xz + 2s₂₃yz = 1}  называется эллипсоидом инерции. Найти:

1.Тензор инерции S.

2.Собственные числа тензора инерции S.

3.Собственные векторы тензора инерции S (все).

4.Базис, в котором множество Э имеет канонический вид.

5.Оси тела D,  вокруг которых оно вращается без вибраций (главные оси эллипсоида инерции).

 

 

Замечания.

 

1.Матрицу А разумнее всего придумать так: придумать несколько элементарных матриц и перемножить их – получится матрица, которую следует считать матрицей А.

 

2. Третью часть ТР рекомендуется делать с помощью математической программы Mapple.

 

3. Типовой расчёт следует защищать по частям. Срок защиты первой части – 9 неделя , второй части -14-я неделя . третьей части – 16-я неделя.

 

4.Студенты, не защитившие типового расчёта, до экзамена не допускаются.

 

Литература.

 

1.Тищенко Н. Матан, Глава 6, лекция 6.

 

 

 

Доцент                              Тищенко Н.