Занятие 1

Множества

 

А.Цель занятия: Усвоить основные теоретико-множественные понятия и, в особенности, понятие n-мерного пространства.

 

Б.Основные факты теории:

 

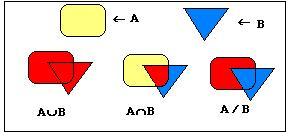
1.Объединение множеств.  È – знак объединения.

xÎ(AÈB)Û(xÎA)Ú(xÎB)

 

2.Пересечение множеств.  Ç – знак пересечения.

xÎ(AÇB)Û(xÎA)Ù(xÎB)

 

3. Разность множеств.         ¤   -  знак разности.

xÎ(A ¤ B)Û(xÎA)Ù(xÏB)

 

Эти три определения иллюстрируются следующим рисунком:

 

4. Декартово произведение множеств.

A₁ x A₂ x …x A_n = {(a₁,a₂,…,a_n)| a₁ÎA₁, a₂ÎA₂, … , a_nÎA_n}.

    Соответственно:

Aⁿ = A x A x …x A = {(a₁,a₂, …, a_n)| a_iÎA, i=1,2,…,n},

                                                          1      2              n

Rⁿ  = R x R x …x R  = {(x₁,x₂, …, x_n)| x_iÎR, i=1,2,…,n}.

 

5. n-мерное пространство.

     Множество Rⁿ  называется n-мерным пространством.  Его можно понимать как множество всех мыслимых энок чисел.

 

В. Задачи.

 

Нарисовать множества:

 

1. . 

 

Ответ: Пять окружностей с центром в начале координат и радиусом 1, ½,  1/3, ¼, 1/5 соответственно.

 

2. .

 

Ответ: Плоское кольцо с малым радиусом ½ и большим радиусом 1.

 

3. .

 

Ответ: Часть круга радиуса 1 с центром в начале координат, лежащего выше прямой

 

L={(x,y)| y=x}.

 

4. A={a,b,c}. X = {1,2,3,4}. M = A x X = ?

 

 

Ответ: M={(a,1),(a,2),(a,3),(a,4),(b,1),(b,2),(b,3),(b,4),(c,1),(c,2),(c,3),(c,4)}.

 

5. M=[0,1] x [0,4].

 

 

Ответ: Прямоугольник  ABCD, где A=(0,0), B=(0,1), C=(1,4), D=(0,4).

 

6..

 

Ответ: Квадрат ABCD,  где A=(-1,-1), B=(1,-1), C=(1,1), D=(-1,1), без круга радиуса ½ с центром в начале координат.

 

7. G=[0,1]² / (0,1)²   .

 

 

Ответ: Граница квадрата ABCD, где A=(0,0), B=(1,0), C=(1,1), D=(0,1).

 

8. M={(x,y)| (x-2)² +y²=1}.

 

 

Ответ: Окружность радиуса 1  с центром в точке (2,0).

 

Далее ответов не будет!

 

9.   .

 

10.  .

 

11.  .

 

12. .

 

13. .

 

 

14. .

 

15. .

 

16. .