Занятие 3

Поверхности в пространстве

 

  А.Цель занятия.

  а.Научиться понимать, что поверхности в пространстве можно задавать в следующих трёх формах:

 

1.P = { (x,y,z) | z = f (x, y) }.

 

2.P = { (x,y,z) | F (x,y,z) = 0 }.

 

3.P = { (x,y,z) | x= F(u,v), y= Y(u,v), z= Х(u,v)}.

 

б.Усвоить также. что если кривая К= { (x,0,z) | x=j (u), z= х(u), uÎ [a,b] }  вращается вокруг оси z, то получится поверхность вращения P,  задаваемая формулой:

 

P= { (x,y,z) | x =j (u)cos(v), y= j(u)sin(v), z= х(u), uÎ [a,b], vÎ [b,c] }

 

Б. Задачи.

 

Нарисовать следующие поверхности:

 

1.P={(x,y,z)| z=x²+y² }

 

Ответ:

 

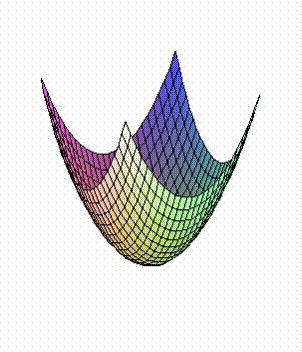
2.P={(x,y,z)| z=x²/a² + y²/b² }

 

3.P={(x,y,z)|  x² + y² + z² = R²}

 

4.P={(x,y,z)| x²/a² + y²/b² – z²/c² = 1 }

 

5.P={(x,y,z)| x²/a² + y²/b² – z²/c² = 0 }

 

6.P={(x,y,z)| x²/a² + y²/b² = 1 }

 

Заданы кривые, вращающиеся вокруг оси z, Нарисовать получающиеся при этом поверхности вращения и задать их формулами. Задать также соответствующие этим поверхностям тела вращения.

 

7.K={(x,0,z)|x=Rcos u,  z=Rsin u, uÎ [-p /2, p /2  }

 

8.K={(x,0,z)| z= x², x>0 }

 

Ответ:

 

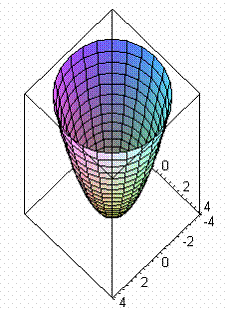
9.K={(x,0,z)| z= e^x, xÎ [0,1] }

 

10.K={(x,0,z)| z= x, xÎ [0,1]  }

 

В.Домашнее задание.

 

Нарисовать поверхности:

 

11.P={(x,y,z)| z= x²/a² – y²/b²  }

 

12.P={(x,y,z)| x²/a² - y²/b² – z²/c² = 1  }

 

13.P={(x,y,z)| x²/a² - y²/b² =1 }

 

Нарисовать поверхности, получающиеся при вращении кривых вокруг оси z:

 

14.K={(x,0,z)| z=(1+x²)^-1 }

 

15.K={(x,0,z)| z= kx }

 

16.K={(x,0,z)| z= sin x, xÎ [0,p] }